在数学的广袤领域中，函数是不可或缺的重要部分，奇函数以其独特的性质在数学中占据一席之地，本文将深入探讨奇函数的性质，旨在帮助读者全面理解奇函数的核心概念及其特性。

奇函数的定义

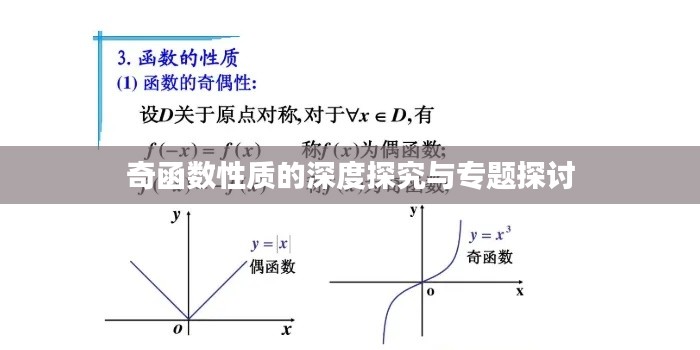
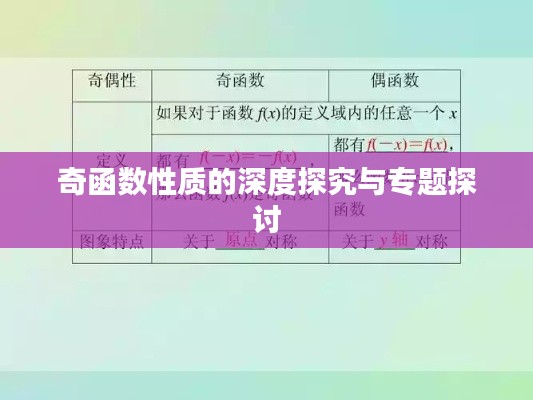
奇函数是定义域关于原点对称的函数，其特性为对于定义域内的任意x，都有f(-x)=-f(x)，这一性质使得奇函数在函数图像上呈现出一种对称性，即函数图像关于原点对称。

奇函数的基本性质

1、奇函数的单调性：奇函数在其定义域内，不一定具有单调性，也就是说，奇函数可能在某些区间内单调递增，而在另一些区间内单调递减，正弦函数在其周期内既包含增区间也包含减区间。

2、奇函数的周期性：并非所有奇函数都具有周期性，一些常见的奇函数如正弦函数和余切函数等，都是周期函数，这些函数的周期性使得它们在特定的周期内重复其特性。

3、奇函数的对称性：如前所述，奇函数的一个重要特性是其对称性，由于奇函数的定义就是关于原点对称，因此其图像也必然关于原点对称，这种对称性在数学中具有重要的应用价值。

4、奇函数的积分性质：对于可积的奇函数，其在一定区间内的定积分值往往具有特殊的性质，对于区间[-a, a]，奇函数的定积分值为零，这一性质在求解积分问题中具有重要的应用价值。

奇函数的应用

奇函数在数学及其他领域具有广泛的应用，在几何学中，我们可以通过奇函数来描述某些图形的对称性；在物理中，许多物理现象（如振动、波动等）可以用奇函数来描述；在工程中，信号处理等领域也会涉及到奇函数的运用，奇函数还在概率论、统计学、计算机科学等领域发挥着重要作用。

常见奇函数示例及其性质

1、正弦函数：正弦函数是周期性的奇函数，其图像是一个在坐标系中波动的曲线，正弦函数在其周期内具有特定的增减性和对称性。

2、余切函数：余切函数也是周期性的奇函数，其图像呈现出一种锯齿状的波动，余切函数的增减性和对称性也与正弦函数类似。

3、符号函数：符号函数是一种非周期性的奇函数，该函数在x=0时取值为零，在其他地方取值为正负一，符号函数的图像呈现出一种折线状。

奇函数作为数学中的重要概念，具有独特的性质和应用价值，本文详细探讨了奇函数的定义、基本性质、应用以及常见示例，希望通过本文的阐述，读者能对奇函数有更深入的理解，并能够在实际问题中灵活应用奇函数的性质，在实际学习和工作中，读者可以根据自身需求和兴趣进一步探索奇函数的更多性质和应用。